前缀和与差分

差分：\(a_1\)、\(a_2\)、\(a_3\)、……、\(a_n\) （下标从 \(1\) 开始）

前缀和：\(S_1\)、\(S_2\)、\(S_3\)、……、\(S_n\) 其中，\(S_i=a_1+a_2+a_3+...+a_i\) （下标从 \(1\) 开始，定义 \(S_0=0\)）

1. 前缀和

1. 涉及到的两个问题

1. 如何求 \(S_i\) ：

   // 一维前缀和的初始化
   for(int i = 1; i <= n; i++)
   	s[i] = s[i - 1] + a[i];		// 前缀和的初始化
   // 二维前缀和的初始化
   for(int i = 1; i <= n; i++)
       for(int j = 1; j <= m; j++)
           s[i][j] = a[i][j] + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];

2. 前缀和数组 \(S_i\) 的作用：快速求出原数组中的一段数的和。

   前缀和数组作用的例子：假设题目要求求出数组中[l, r]的数的和（区间和的计算）

   • 如果没有前缀和数组，则需循环一遍求解，此时时间复杂度为 \(O(n)\)
   • 如果有前缀和数组，则可直接计算得出 \(S_r-S_{l-1}\)，此时时间复杂度为 \(O(1)\)

2. 为什么前缀和的下标从1开始

主要是处理边界问题：当需要求数组[1, t]的数的和的时候，可以直接通过 \(S_t-S_0\)，不用考虑边界问题。同时，这也是把 \(S_0\) 定义为 \(0\) 的原因。虽然该问题可以直接以 \(S_t\) 为答案，但是为了统一计算公式，选择这种计算方法。

1.1 一维前缀和

作用：快速求出某一区间的和

原数组：\(a_i\)

前缀和数组：\(S_i\)

区间和计算公式：\([l,\ r]=S_r-S_{l-1}\)

S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]

1.2 二维前缀和

与一维前缀和类似，二维前缀和是为了快速求出某一子矩阵的和

原数组：\(a_{ij}\)

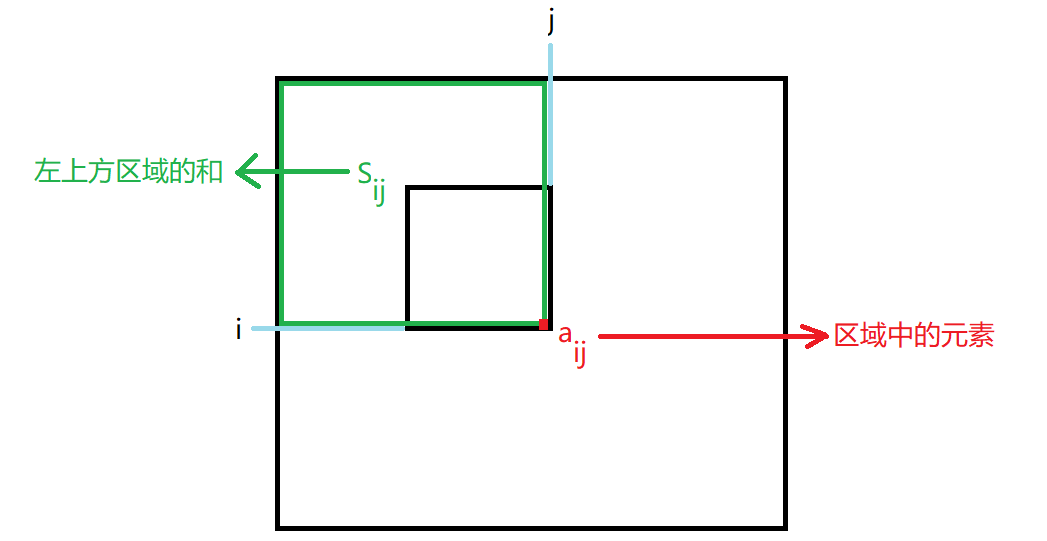
前缀和数组：\(S_{ij}\)

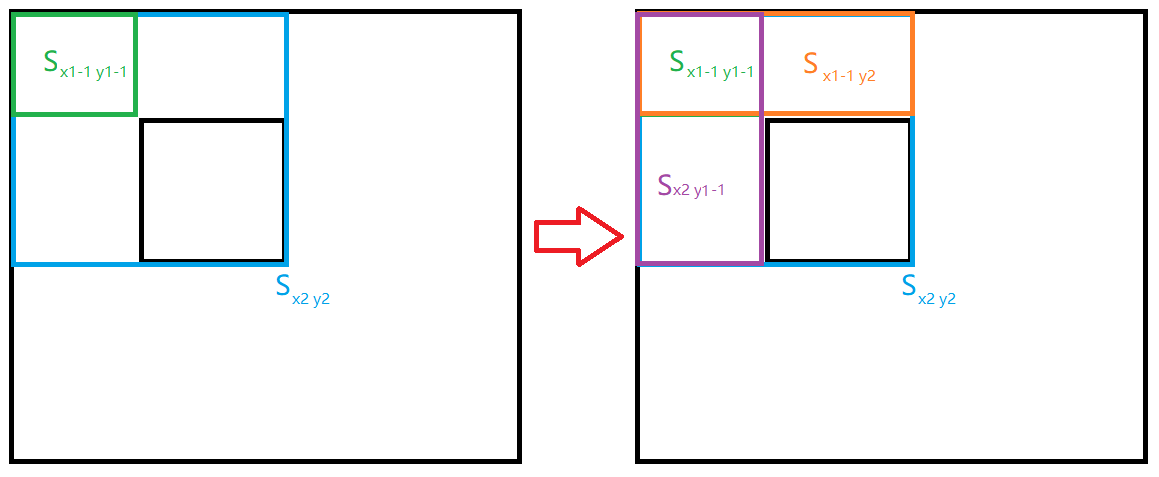
子矩阵和计算公式： \[ \left[ \begin{matrix} \left( x_1, y_1 \right)& \left( x_1, y_2 \right)\\ \left( x_2, y_1 \right)& \left( x_2, y_2 \right)\\ \end{matrix} \right] =S_{x_2y_2}-S_{x_1-1 y_2}-S_{x_2\,\,y_1-1}+S_{x_1-1 y_1-1} \]

S[i, j] =  	// 第i行j列格子左上部分所有元素的和
// 以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

2. 差分

1. 差分的作用

对于数组 \(a_i\ (i=1,2,3,…,n)\)，其前缀和为 \(s_i\ (i = 1,2,3,…,n)\)。\(a_i\) 为 \(s_i\) 的差分，满足 \(a_i\ = s_i \ - \ s_{i-1}\)，即： \[ a_1 = s_1\\ a_2 = s_2-s_1\\ a_3 = s_3-s_2\\ a_4 = s_4-s_3\\ ……\\ a_n = s_n-s_{n-1} \] 作用：对于前缀和数组 \(s_i\) ，如果需要使其从第 \(l\) 项开始到第 \(r\) 项每项都增加一个常数 \(C\) 。如果直接对前缀和数组 \(s_i\) 操作的话，即对 \(s_i\ (i = l,l+1,…,r)\) 每一项都增加一个常数 \(C\)，程序的时间复杂度为 \(O(n)\)；如果对差分数组 \(a_i\) 操作的话，即使 \(a_l + C\) 、\(a_{r+1} - C\)，程序的时间复杂度为 \(O(1)\)。

2.1 一维差分

作用：给一维数组的一段加上一个值

给区间[l, r]中的每个数加上c：B[l] += c, B[r + 1] -= c

过程：

1. 定义前缀和数组，并输入初值（给 \(s_i\) 赋初值）

2. 根据前缀和数组的值，给差分数组赋初值（给 \(a_i\) 赋值）

   对于差分数组中的第 \(i\) 个元素，采用插入的方式：对于区间[i,i]插入s[i]，即a[i] + s[i]、a[i+1] - s[i]

3. 根据差分数组，求出其前缀和即可

2.2 二维差分

作用：给二维数组数组的一个子矩阵加上一个值

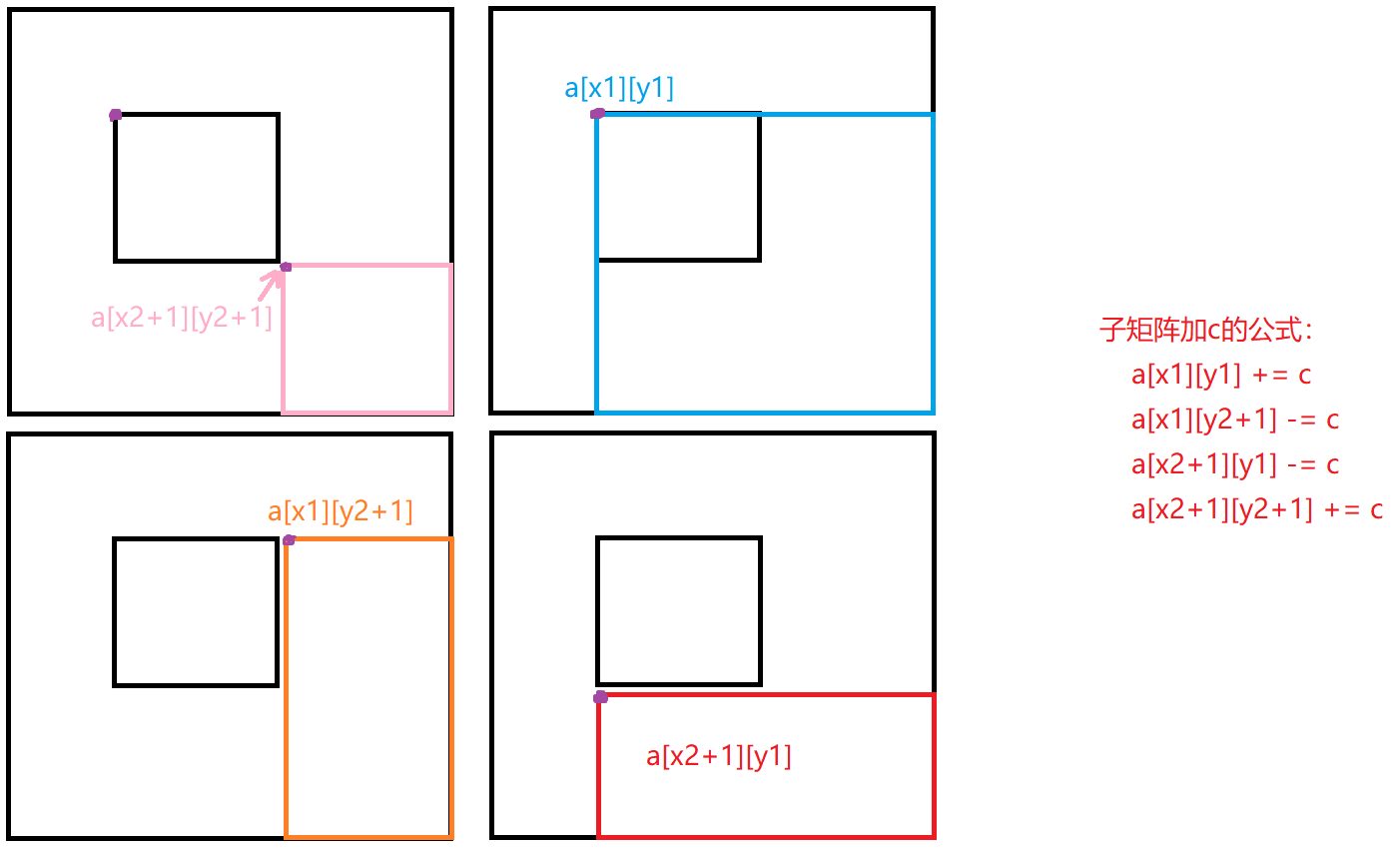
给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

过程同一维差分，只不过计算差分数组的方式不同